ホーム> 私立中学受験サポートページ > 私立中学入試対策算数（場合の数④ 立方体の辺の道順）

私立中学入試対策算数（場合の数④ 立方体の辺の道順）

問題

(難易度★★★★☆）

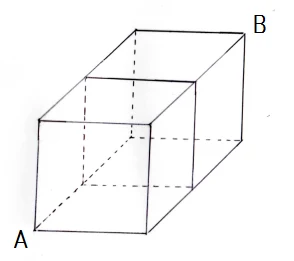
上の図は、同じ大きさの立方体を２つ組み合わせたものです。実線または点線を通って、ＡからＢへ行く最短の行き方は、全部で何通りでしょうか。

プリントのダウンロードは、私立中学受験サポートページから。

これまでは平面上にある碁盤目状の道の通り方だったのに対して、今回は立方体になります。立方体になったからと言って、何か解き方が変わったわけではなく、碁盤目状の道と同様に最短ルートを数えていけばＯＫです。

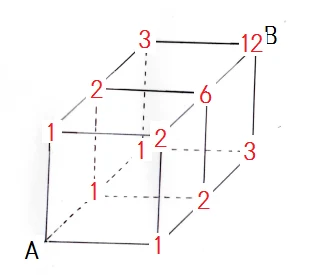
上の図のようにＡから上、右、奥に1辺分だけ移動した頂点にそれぞれ1と書きます。これは、その頂点までの道順は、Ａ地点からのみということを表します。あとは足し算をしていくだけ。

Ｂ地点は１２となるので、答えは「12通り」です。

これに似た問題が、上智福岡中学校の入学試験に出題されていました。そちらは立方体を横に並べていました。解き方さえ知っていれば、それほど難しい問題ではありません。

私立中学校を目指す生徒で、算数が苦手な子が少なくありません。算数に不安がある方は、お気軽にご相談してください。

(2017.09.05更新)

関連記事

・私立中学入試対策算数（場合の数① 碁盤目状の道順基礎）

・私立中学入試対策算数（場合の数④ 立方体の辺の道順）(このページ)