私立中学入試対策算数（場合の数② 1地点をかならず通る道順）博多女子中学校上智福岡中学校自彊館中学校弘学館中学校中学受験│福岡で直接契約・個人契約のプロ家庭教師

ホーム> 私立中学受験サポートページ > 私立中学入試対策算数（場合の数② 1地点をかならず通る道順）

私立中学入試対策算数（場合の数② 1地点をかならず通る道順）

問題

(難易度★★★☆☆）

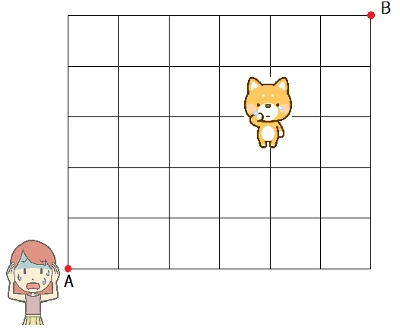
上の図のような碁盤目の形をした道がある。ヒロミさんは散歩中に愛犬チャッピーとはぐれてしまった。Ａ地点を出発し、チャッピーと合流しＢ地点に行くとき、もっとも短い道のりで行ける道順は何通りあるか。

プリントのダウンロードは、私立中学受験サポートページから。

解答・解説

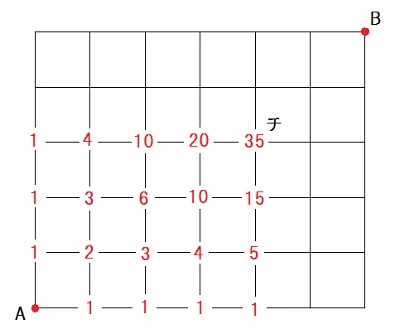
まずは下の図のように、Ａ地点からチャッピーがいる場所までの最短ルートを数えます。すると35通りということがわかります。

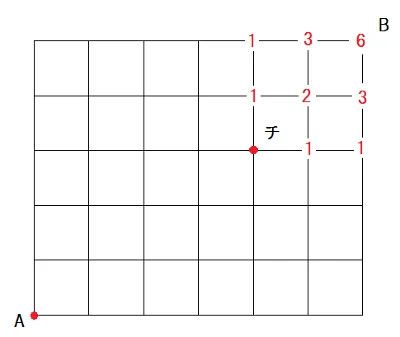
つぎにチャッピーのいる場所からＢ地点までの最短ルートを数えます。6通りです。

Ａ地点からチャッピーまでが35通り、チャッピーと出会ってからＢ地点までが6通りなので、Ａ地点からチャッピーがいる道を通り、Ｂ地点に行く道順は、「35×6＝210」となります。

したがって、答えは「210通り」です。

おわりに

碁盤目状の道の問題は、今年（2017年）の上智福岡中学校の入試問題に出題されていました。それ以外の中学校でも、比較的に出題頻度の高い問題と言えます。いろいろな種類の問題を解いてみましょう。

私立中学校を目指す生徒で、算数が苦手な子が少なくありません。算数に不安がある方は、お気軽にご相談してください。

(2017.09.04更新)

関連記事

・私立中学入試対策算数（場合の数① 碁盤目状の道順基礎）

・私立中学入試対策算数（場合の数② 1地点をかならず通る道順）(このページ)