【令和5年】博多女子中 特待選抜入試 算数|解説と対策
このページでは、博多女子中学校の令和5年度「特待選抜入試(算数)」の全問題を解説しています。
特待選抜入試に向けた勉強法や注意点は以下のページの内容を参考にしてください。 【算数攻略法】博多女子中・特待選抜入試 対策ポイント
第1問 計算問題集合
(予想配点 3点×10問)
(1)
\[ \begin{align} 278-336+516 &= 278+516-336\\ & = 794-336 \\ &=458 \end{align} \]
(2)
\[ \begin{align} 70-85\div5 &=70-17\\ &=53\ \end{align} \]
(3)
\[ \begin{align} &1\dfrac{~\lower0.3ex\hbox{$1$}~} {\lower0.3ex\hbox{$2$}} \times 2\dfrac{~\lower0.3ex\hbox{$2$}~} {\lower0.3ex\hbox{$3$}} \div 3\dfrac{~\lower0.3ex\hbox{$3$}~} {\lower0.3ex\hbox{$4$}}\\ =&\dfrac{~\lower0.3ex\hbox{$3$}~} {\lower0.3ex\hbox{$2$}} \times \dfrac{~\lower0.3ex\hbox{$8$}~} {\lower0.3ex\hbox{$3$}} \times \dfrac{~\lower0.3ex\hbox{$4$}~} {\lower0.3ex\hbox{$15$}}\\ =&\dfrac{~\lower0.3ex\hbox{$3 \times 8 \times 4$}~} {\lower0.3ex\hbox{$2 \times 3 \times 15$}}\\ =&\dfrac{~\lower0.3ex\hbox{$16$}~} {\lower0.3ex\hbox{$15$}} \end{align} \]
(4)
\[ \begin{align} 9.87 \times 1.2 =11.844 \end{align} \]
(5)
\[ \begin{align} &23-(3+2 \times 9) \div 7\\ =&23-21\div7 \\ =&23-3\\ =&20\\ \end{align} \]
(6)
\[ \begin{align} &80 \div (21-5) \times 2.4 \\ =&80 \div 16 \times 2.4 \\ =&\dfrac{~\lower0.3ex\hbox{$80 \times 1 \times 24$}~} {\lower0.3ex\hbox{$1 \times 16 \times 10$}}\\[8pt] =&12 \end{align} \]
(7)
\[ \begin{align} & \left (1-\dfrac{~\lower0.3ex\hbox{$1$}~} {\lower0.3ex\hbox{$2$}} \right) \times \left (1-\dfrac{~\lower0.3ex\hbox{$1$}~} {\lower0.3ex\hbox{$3$}} \right) \times \left (1-\dfrac{~\lower0.3ex\hbox{$1$}~} {\lower0.3ex\hbox{$4$}} \right) \\ &\times \left (1-\dfrac{~\lower0.3ex\hbox{$1$}~} {\lower0.3ex\hbox{$5$}} \right) \\ =&\dfrac{~\lower0.3ex\hbox{$1$}~} {\lower0.3ex\hbox{$2$}} \times \dfrac{~\lower0.3ex\hbox{$2$}~} {\lower0.3ex\hbox{$3$}} \times \dfrac{~\lower0.3ex\hbox{$3$}~} {\lower0.3ex\hbox{$4$}} \times \dfrac{~\lower0.3ex\hbox{$4$}~} {\lower0.3ex\hbox{$5$}}\\ =&\dfrac{~\lower0.3ex\hbox{$1$}~} {\lower0.3ex\hbox{$5$}} \end{align} \](8)
\[ \begin{align} &\dfrac{~\lower0.3ex\hbox{$10×9×8×7$}~} {\lower0.3ex\hbox{$18$}}-\dfrac{~\lower0.3ex\hbox{$6×5×4×3$}~} {\lower0.3ex\hbox{$15$}}\\ =&280-24\\ =&256 \end{align} \]
(9)
\[ \begin{align} &\left (1.55+\dfrac{~\lower0.3ex\hbox{$1$}~} {\lower0.3ex\hbox{$4$}}\right) -3 \times \dfrac{~\lower0.3ex\hbox{$3$}~} {\lower0.3ex\hbox{$5$}} \\ =&(1.55+0.25)-\dfrac{~\lower0.3ex\hbox{$9$}~} {\lower0.3ex\hbox{$5$}}\\ =& 1.8-\dfrac{~\lower0.3ex\hbox{$9$}~} {\lower0.3ex\hbox{$5$}}\\ =& \dfrac{~\lower0.3ex\hbox{$9$}~} {\lower0.3ex\hbox{$5$}} - \dfrac{~\lower0.3ex\hbox{$9$}~} {\lower0.3ex\hbox{$5$}}\\ =& 0 \end{align} \]
(10)
\[ \begin{align} & 21 \div \left( 7.24- \dfrac{~\lower0.3ex\hbox{$6$}~} {\lower0.3ex\hbox{$25$}}\right) - 2 \\ =& 21 \div (7.24-0.24)-2 \\ =& 21 \div 7-2 \\ =& 3-2 \\ =& 1 \end{align} \]
第2問 文章問題集合
(予想配点 3点×7問)
(1)
\[25200秒=25200 \div 60=420分\] \[420分=420 \div 60 = 7時間\]
\[ \underline{ 答え 7時間} \]
(2)
\[ \begin{align} &7で割っても,12で割ってる,3余る \\ → &7と12の最小公倍数+3 \\ → &84の倍数+3 \end{align} \]
\[150 \div 84 =1あまり66\] \[84 \times 1+3=87\] \[84 \times 2+3=171\] \[150に近い整数は171\] \[ \underline{ 答え 171} \]
(3)
\[ 3割の利益を見込む→1.3倍 \] \[ 原価を□円とすると \]
\[ \begin{align} □\times 1.3-100&=940\\ □\times 1.3&=940+100=1040\\ □&=1040 \div 1.3=800 \end{align} \]
\[ \underline{ 答え 800円} \]
(4)
\[水:食塩=17:3だから\] \[食塩水:食塩=20:3 \] \[\dfrac{~\lower0.3ex\hbox{$3$}~} {\lower0.3ex\hbox{$20$}} \times 100 =15\] \[ \underline{ 答え 15%} \]
(5)
\[時間= \frac{距離}{速さ}\]
\[40 \div 90 = \frac{40}{90}= \frac{4}{9}時間\]
\[
\begin{align}
\frac{4}{9}時間 &= \frac{4}{9} \times 60 \\
&=\frac{80}{3} \\
&=26\frac{2}{3} \\
&=26分40秒
\end{align}
\]
\[ \underline{ 答え 26分40秒} \]
(6)
\[4回目までの合計\;72\times4=288\] \[3回目までの合計\;288-78=210\] \[3回目までの平均\; 210 \div 3=70\] \[72-70=2\] \[ \underline{ 答え 2点} \]
(7)
\[4時間=240分\] \[ \begin{align} A \quad &40:240=25:a\\ &a=25 \times6=150 \end{align} \] \[ \begin{align} B \quad &60:240=40:b\\ &b=40 \times4=160 \end{align} \] \[150+160=310\]
\[ \underline{ 答え 310個} \]
第3問 規則性
(予想配点 4点×3問)
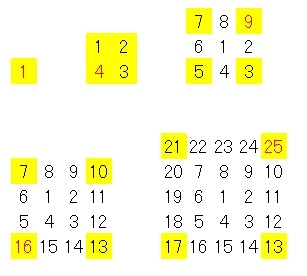
(1)
\[ 縦□列、横□列の最も大きい数字は □\times□ \]
\[ 縦6列、横6列の最も大きい数字は 6\times6=36 \]
\[ \underline{ 答え 36} \]
(2)
縦□列、横□列の4つの角にある数字で最も大きい整数は\(□\times□\)。
残りの3つの整数は、最も大きい数から□-1を引いていくことで求めることができる
縦8列、横8列の4つの角の整数は大きい順に
\( 8 \times 8=64\),
\( 64-(8-1)=64-7=57\),
\( 57-7=50\),
\( 50-7=43 \)
4つの整数の合計は\( 64+57+50+43=214\)
\[ \underline{ 答え 214} \]
(3)
\( 10 \; \fbox{ア} \; 13 \; \fbox{イ} \; 7 \; \fbox{ウ} \; 16 \; \fbox{エ} \; 1=85 \)
\( +, \; -, \; \times, \; \div \) のうち答えが整数であるから,\(\fbox{エ}\)に\(\div\)が入る
\( 10\times13=130\), \(13\times7=91\), \(7\times16=112\)より
\( \fbox{イ}\) に\(\times\) が入る(130,112は85から離れすぎ)
よって, \( \fbox{ア}\)に\( +\), \( \fbox{ウ}\)に\( -\)が入る
\[ 10 \; + \; 13 \; \times \; 7 \; - \; 16 \; \div \; 1=85 \]
\[ \underline{ 答え ④} \]
第4問 平面図形
(1)(予想配点 3点×3問)
①
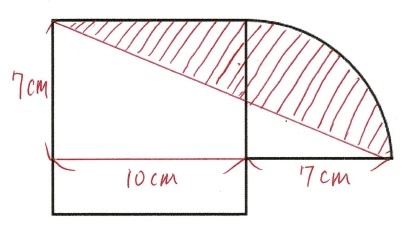
\[求める面積は、長方形 + 四分円 - 三角形\]
\[長方形=7 \times 10=70\]
\[四分円=7 \times 7 \times 3.14 \div 4=38.465\]
\[三角形=7 \times 17 \div 2=59.5 \]
\[70+38.465-59.5=48.965 \]
\[ \underline{ 答え 48.965cm^2} \]
②
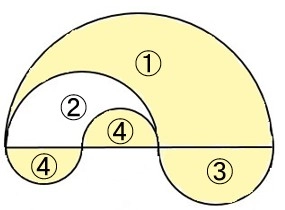
※注意
円やおうぎ形の問題は、円周率の計算は最後に行う
周の長さ
\[求める長さは、\]
\[(半円①+半円②+半円③の弧+円④の円周)\]
\[+円④の直径\times2\]
\[半円①=14 \times 3.14 \div2 =7\times 3.14\]
\[半円②=8\times 3.14 \div2 =4\times 3.14\]
\[半円③=6 \times 3.14 \div2 =3\times 3.14\]
\[円④=4\times 3.14\]
\[よって、まわりの長さは\]
\[ \begin{align} &(7+4+3+4)\times 3.14 +4 \times 2\\ =&56.52+8 \\ =&64.52 \\ \end{align} \]
\[ \underline{ 答え 64.52cm} \]
面積
\[求める面積は、半円①+半円③+円④-半円②\]
\[半円①=7 \times 7 \times 3.14 \div2 =24.5\times 3.14\]
\[半円③=3 \times 3 \times 3.14 \div2 =4.5\times 3.14\]
\[円④=2 \times 2\times 3.14=4\times 3.14\]
\[半円②=4 \times 4\times 3.14 \div2 =8\times 3.14\]
\[ \begin{align} &①+③+④-②\\ =&(24.5+4.5+4-8)\times 3.14 \\ =&25 \times 3.14 \\ =& 78.5 \end{align} \]
\[ \underline{ 答え 78.5cm^2} \]
(2)(予想配点 4点×1問)
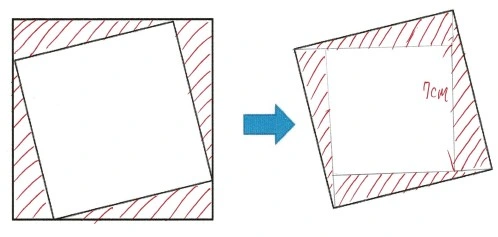
\[7 \times 7=49 \]
\[ \underline{ 答え 49cm^2} \]
(3)角度(予想配点 4点×2問)
㋐
\[㋐= 62+37+32=131\]
\[ \underline{ 答え ㋐ = 131^\circ} \]
㋑
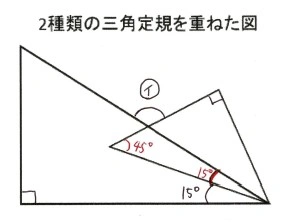
\[30-15=15\]
\[180-(45+15)=120\]
\[ \underline{ 答え ㋑=120^\circ} \]
第5問 空間図形
(予想配点 4点×4問)
(1) (体積)
頂点スとセが重なる点をそれぞれ求めれば良い。
立方体の重なる点の求め方
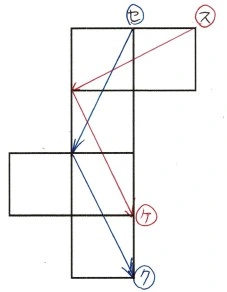
① 点スから、展開図上で隣の正方形に向けて対角線を1本引く
② その正方形からもう一つ隣の正方形へと、同様に対角線を引く
③ 最後にたどり着いた点ケが、点スと重なる点になる
上の方法で点スと点セが重なる点を求めると、点ケと点クになる。よって、辺スセと重なる辺は、辺クケ。
\[ \underline{ 答え 辺クケ} \]
(2)
\[ \underline{ 答え ④} \]
(3)
(体積)
上から1段目には立方体が1個
2段目には立方体が1+2=3個
3段目には立方体が3+3=6個
4段目には立方体が6+4=10個
よって、積み上げた立体には、
1+3+6+10=20個の立方体が使われている
立方体は1辺が3cmであるから、1つの立方体の体積は、
\(3 \times 3 \times 3=27(cm^2)\)
よって、求める立体の体積は、 \(27 \times 20 = 540\)
\[ \underline{ 答え 540cm^3} \]
(表面全体の面積)
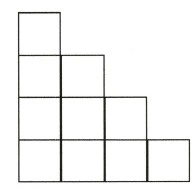
\[この立体を、上下、前後、左右の方向からみると\] \[すべて上の形に見える。\]
\[また6方向から見ると、すべての面が見えるため、\] \[上の図形の面積\times 6 をすることで\] \[立体の表面全体の面積を求めることができる。\]
\[3\times3 \times 10=90\]
\[90\times 6 =540\]
\[ \underline{ 答え 540cm^2} \]
おわりに
令和5年度の問題は、思考のプロセスを丁寧にたどることで確実に得点できる内容が多く出題されました。 今年度の入試との比較や、自分の理解度のチェックとして過去問を活用するのがおすすめです。 基礎~標準問題をしっかり固め、出題形式に慣れることが特待合格への近道です。
◇家庭教師ふなきちのサービスの特徴◇
- 完全1対1だから「わかる!」「できる!」
- 15年間で培った高い指導力・豊富な経験則
- 指導料と交通費だけ!安心な料金体系!
- 教材販売なし!配布プリントは完全無料!
◇こんな生徒さんにおすすめ!◇
- 「難関校の算数の問題が上手く解けない」
- 「塾での成績が伸び悩んでいる」
- 「習い事と両立しながら中学受験したい」
- 「苦手教科を集中的に克服したい」
無料体験授業も実施中です!
まずは トップページ をご覧いただき、サービス内容をご確認ください。
◇関連ページ◇
特待生制度、受験対策、受験スケジュールなどを詳しくまとめています。
博多女子中学校の受験準備を進める際には、まず全体の特徴を把握し、その後、具体的な指導例も参考にしてください。


