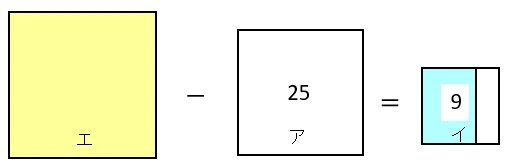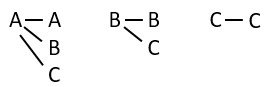【2024年度】西南学院中 入試問題 算数｜解説と対策

\[ \begin{align} (1)&4\times15-(18-2\times3)\div4\\ =&60-35\div4\\ =&57 \end{align} \]

\[ \underline{ 答え　57　} \]

\[ \begin{align} (2)(3-□\times0.2)\times0.25=0.6 \end{align} \] \[ \begin{align} (3-□\times \frac{1}{5})\times \frac{1}{4}=\frac{3}{5} \end{align} \] \[ \begin{align} 3-□\times \frac{1}{5}=\frac{3}{5}\div \frac{1}{4}=\frac{12}{5} \end{align} \] \[ \begin{align} □\times \frac{1}{5}&=3-\frac{12}{5}=\frac{3}{5} \end{align} \] \[ \begin{align} □&=\frac{3}{5} \div \frac{1}{5}=3 \end{align} \]

\[ \underline{ 答え　3　} \]

(3)

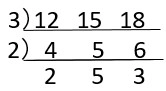
12,15,18の最小公倍数は
\(2\times2\times3\times3\times5=180\)

\[ \underline{ 答え　180　} \]

(4)

上の図のように問題文に書かれている内容から混ぜた後の食塩水の質量と食塩の質量を求める。
混ぜた後の食塩水の質量は300gで溶けている食塩の質量は27gだから、その濃度は

\[ \begin{align} □=\frac{27}{300}\times 100=9 \end{align} \]

\[ \underline{ 答え　9％　} \]

(5)
仕入れ値　400円
定価　仕入れ値の3割上乗せ→\(\dfrac{130}{100}\)倍
売値　低下の20%引き→\(\dfrac{80}{100}\)倍

売った値段は、

\[ \begin{align} 400\times \frac{130}{100} \times \frac{80}{100}=416 \end{align} \]

\[ \underline{ 答え　416円　} \]

(6)

底辺の長さが\(x~cm\),高さが\(y~cm\)の三角形の面積が\(15cm^2\)だから
\(x\times y\div2=15\)
yをxの式であらわすと

\[ \begin{align} x\times y\div2&=15\\ x\times y &=15 \times2=30\\ y&=30\div x \end{align} \]

\[ \underline{ 答え　30\div x　} \]

(7)

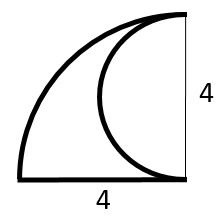
太線の周の長さは、
半径2cmの半円の弧（こ）の長さ
半径4cmの四分円の弧の長さ
4cmの直線
で構成されている。

\[ \begin{align} &8\times3.14\div4+4\times3.14\div2+4\\ =&2\times3.14+2\times3.14+4\\ =&4\times3.14+4\\ =&12.56+4\\ =&16.56 \end{align} \]

\[ \underline{ 答え　16.56cm} \]

(8)

水そうを図のように、\(20cm\times40cm\times10cm\)の直方体と\(20cm\times10cm\times10cm\)の直方体に分ける。

この水そうに１分間に\(200cm^2\)の割合で水を入れると水面の高さは、\(20\times40\times10\)の直方体の容積が満たされるまでは一定で高くなり、 その後は\(20\times10\times10\)の直方体の容積が満たされると満水になる。

よって、その時間を求めると

\[ \begin{align} &20\times40\times10\div200\\ =&8000\div 200\\ =&40\\ \end{align} \]

\[ \begin{align} &20\times10\times10\div200\\ =&2000\div 200\\ =&10\\ \end{align} \]

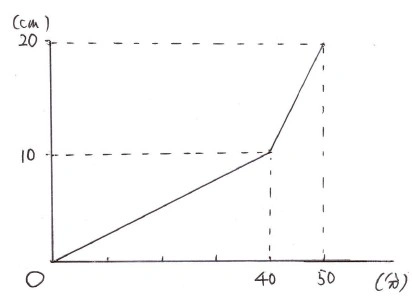
水面の高さは、水を入れ始めて40分で10cmまで上がり、さらに10分で20cmまで上がって、満水となる。 よって、グラフは下の通りとなる。

(1)

\[ \begin{align} &\left( \frac{176}{2024} +□ \right) \div \left( \frac{3}{4} +\frac{1}{8} \right)=\frac{4}{23}\\ &\left( \frac{2}{23} +□ \right) \div \frac{7}{8}=\frac{4}{23}\\ &\frac{2}{23} +□=\frac{4}{23}\times\frac{7}{8}=\frac{7}{46}\\ &□=\frac{7}{46}-\frac{2}{23}=\frac{3}{46} \end{align} \]

\[ \underline{ 答え　\frac{3}{46}　} \]

(2)

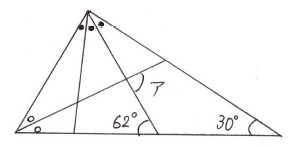
(印がついているところは同じ角度)

アの角は外角の定理より
\(ア=62+〇\)

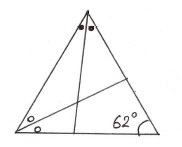
上の図より
\(〇+●=(180-62)\div2=118\div2=59\)

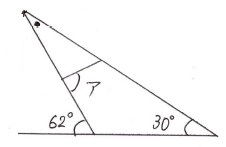
●は外角の定理より
\(●=62-30=32\)

\(○+●=59\)で　\(●=32\)だから
\(○=59-32=27\)

\(ア=62+〇\)で　\(〇=27\)だから
\(ア=62+27=89\)

\[ \underline{ 答え　89^\circ　} \]

(3)

□番目のマッチ棒を増やす本数は
\(□\times2+2\)本であるから順に表に書き入れていくと
⑦番目は70本必要なのがわかる

\[ \underline{ 答え　70本　} \]

(4)

まず、展開図に頂点の記号（アルファベット）を記入する。

展開図に頂点を記入するときのコツ

①　展開図で90度回転したときに重なる頂点は同じ記号になる

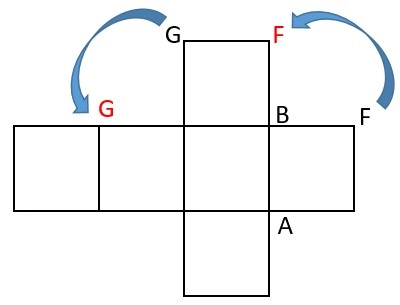
②　見取り図でもっとも遠い2つの頂点を展開図上で結ぶと、正方形2つをならべてできる長方形の対角線となる たどり着いた頂点と最初の頂点は同じ記号になる

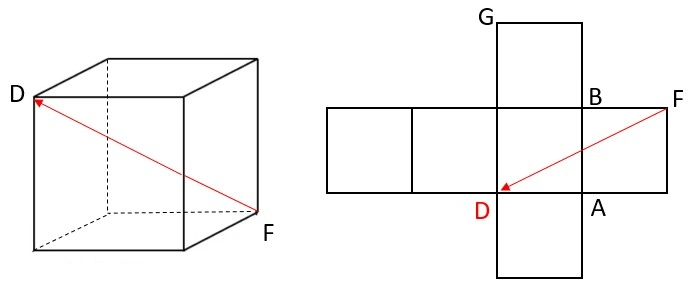
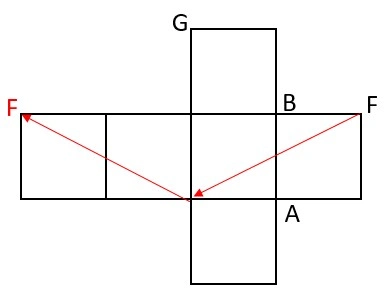
③　展開図上で隣の正方形に向けて対角線を引き、さらに隣り合う正方形に向けて対角線を引いたとき、 たどり着いた頂点と最初の頂点は同じ記号になる

展開図にすべての頂点を記入すると下の図の通りになる

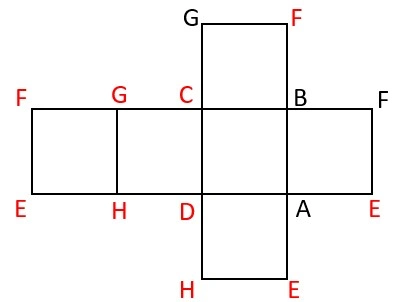
問題の図1の立方体の表面の線を書き入れと下の図になる。

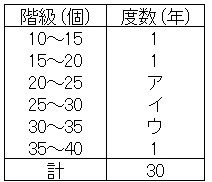
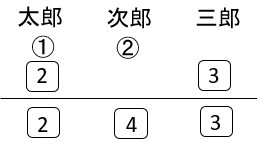
(1)

「正」の字を書いて、慎重に数え上げていく。その際、一度数えたものは一つ一つしっかりと消すことを忘れずに！

\[ \underline{ 答え　ア　12　イ　13　ウ　2　} \]

(2)

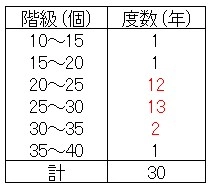
今回、データの数が30であるため、その中央値は小さいほうから15番目と16番目のデータの平均値である。 度数分布表とデータを見ると、小さいほうから数えて15番目は、25個以上30個未満の階級の最小値であるから25個、 16番目は26個であることがわかる。

よって、中央値は\((25+26)\div2=25.5\)

\[ \underline{ 答え　25.5個　} \]

(3)
2021年と2022年のデータを加えると

2つのデータが増えたことにより、その中央値は小さいほうから16番目と17番目の平均値となる。 ①から中央値が25個となるため、16番目と17番目はどちらも25個ということになり、 2021年と2022年に発生した台風はどちらも25個以下であり、さらに少なくとも1つは25個であることがわかる。

②より2013年から2022年の10年間の台風の個数の平均が26.2であるから、合計の個数は\(26.2\times10=262\)。 資料から2013年から2022年に発生した台風の個数の合計は215であるため、2021年と2022年に発生した台風の合計は、 \(262-215=47\)個となる。

2021年と2022年の少なくとも1つは25であるから、\(47-25=22\)となり、③より2021年の個数が少ないから 2021年に発生した台風の個数は22個とわかる。

\[ \underline{ 答え　22個　} \]

(1)

正方形アの1辺の長さは5cm、正方形イの一辺の長さは3cm。
上の図の正方形ア、イ、ウを並べた図形の周の長さは30cm。

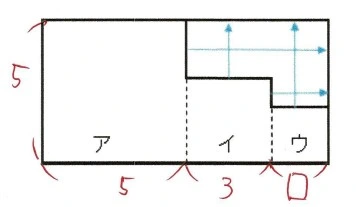
この図形の辺を移動すると、上図のように長方形となる。

長方形の周の長さの求め方は、
\((たて+よこ)\times2\)　
である。

ウの一辺の長さを□cmとすると、
上の図の長方形のたての長さは5cm、横の長さは(5+3+□)cmであるから、

\[ \begin{align} \left \{ 5+(5+3+□)\right \} \times2&=30\\ 13+□&=30\div2=15\\ □&=15-13=2 \end{align} \]

\[ \underline{ 答え　2cm} \]

(2)

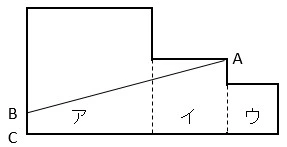
直線ABによって図形の面積が2等分されており、 BCを含む図形は、台形と一辺が2cmの正方形が組み合わさった図形である。

3つの正方形が組み合わさった図形の面積は

\[ \begin{align} & 5\times5+3\times3+2\times2 \\ =& 25+9+4 \\ =&38 \end{align} \]

この図形が2等分されているので、
\(38 \div 2=19 \)

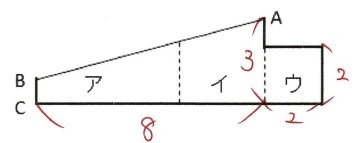
BCの長さを□cmとすると

\[ \begin{align} (□+3)\times8\div2+4&=19 \\ (□+3)\times8\div2&=19-4=15 \\ (□+3)\times8&=15\times2=30 \\ □+3&=30\div8=3.75\\ □&=3.75-3=0.75 \end{align} \]

\[ \underline{ 答え　0.75cm　} \]

(3)

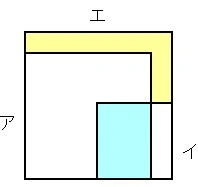
過去問掲載サイトでは印刷の関係でちょっと醜いのですが、 一辺の長さがわからない正方形エと正方形ア、イを組み合わせると、 図の水色と黄色部分の面積が等しいとき、正方形エの面積を求める。

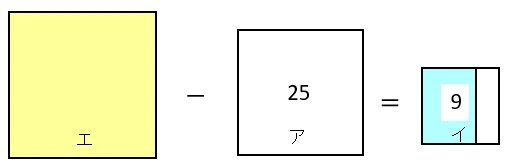
図から「エからアを引いた面積」と「イの面積が等しい」ことがわかる。

よって、エの面積を\(□cm^2 \)とすると、

\[ \begin{align} □-25&=9 \\ □&=9+25=34 \\ \end{align} \]

\[ \underline{ 答え　34cm^2　} \]

(1)

太郎と三郎は、太郎が15分間で進む距離を向かいあって出発し、6分後に出会う。 このことから、三郎の6分間で歩いた距離は、太郎が9分間で進む距離ということがわかる。 つまり、太郎と三郎の速さの比は、\(6:9=2:3\)である。

同じ距離を歩くときにかかる時間の比は、速さの比の逆比であるから、 太郎と三郎がスタート地点に戻ってくる時間の比は、\(3:2\)である。

\[ \begin{align} 3:2&=15:□ \\ □&=2\times5=10 \\ \end{align} \]

\[ \underline{ 答え　10分後　} \]

(2)　

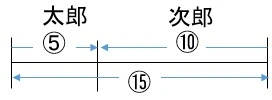
(1)と同様に太郎と次郎の速さの比を求めると、\(5:10=1:2\)である。

太郎と次郎の速さの比　1：2
太郎と三郎の速さの比　2：3

このままでは次郎と三郎の速さの比がわからないので、 比の共通化（連比）を行う。

よって、太郎と次郎と三郎の速さの比は、2：4：3である。

次郎の速さをもとにしたときの三郎の速さの割合は、
\(3 \div 4=\dfrac{3}{4}\)

\[ \underline{ 答え　\dfrac{3}{4}倍　} \]

(3)

太郎と次郎と三郎の速さの比は、2：4：3であるから、池の周りを1周する時間の比は、
\(\dfrac{1}{2} : \dfrac{1}{4} : \dfrac{1}{3} =6 : 3 : 4\)

太郎は池の周りを1周するのに15分間かかる。このことから他の2人が1周するのにかかる時間を求めると、

次郎　\(15 \div \dfrac{3}{6}=\dfrac{15}{2}=7.5\)(分)
三郎　\(15 \div \dfrac{4}{6}=10\)(分)

はじめに出発してから3人がすれちがうまでの様子をグラフにかく。

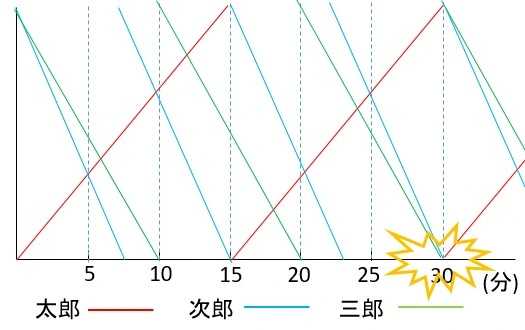
グラフより出発してから30分後にはじめて3人がすれ違うことがわかる。 このとき、三郎は池を3周していて、池のまわりの長さは1000mであるから、三郎の歩いた距離は
\(1000\times3=3000\)(m)

\[ \underline{ 答え　3000m　} \]

(1)

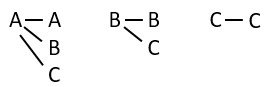
\[ \underline{ 答え　6通り　} \]

(2)　

5個の商品をセットで買うとき、代金は2200円となる。

5個のAを単品で買うとき、
\(480 \times 5=2400\)円となる。

Aを1つだけBといれかえると、代金は\(480-440=40\)円安くなり、
また、Aを1つだけCといれかえると、代金は\(480-360=120\)円安くなる

このことから、5個のAをいくつかB,Cと入れ替えて200円分安くなるようにすれば、セットで購入したときと代金が等しくなる。

\(200=40+40+40+40+40\)から、Aを5つともBといれかえると2200円となる。

また、\(200=40+40+120\)から、5つのAから、2つをBに、1つをCにいれかえると2200円となる。

\[ \underline{ 答え　 \begin{cases} A→0　B→5　C→0\\ A→2　B→2　C→1 \end{cases} 　} \]

(3)

A　4個,　B　5個,　C　2個を購入するときもっとも安くなる方法は

高い商品からセットで買うと安くなるから、A4個、B1個を単品で購入する時の代金を計算すると、
\(480\times4+440=2260\)となり、これらの商品はセットで購入したら安くなる。

次に、B4個、C1個を単品で買う時の代金を計算すると、
\(440\times4+360=2120\)となり、これらの商品は単品で購入するほうが安くなる。

よって、セット(A4個,B1個)を1セット、Bが4個とCが2個を単品で購入するとき、最も安くなる。 その代金を計算すると

\[ \begin{align} &2200\times440\times4+360\times2\\ =&2200+1760+720\\ =&4680 \end{align} \]

\[ \underline{ 答え　4680円　} \]